由Michel Levis

应用工程师| Quanser Inc.

在本文中，我想更深入地研究仪器和建模领域，在其中我们添加了四个新的实验室实验：参数估计，频率响应，状态空间建模和摩擦识别。

为什么要使用仪表

仪器仪表是一门测量和控制过程变量的科学。这是一个与控制和工业自动化有关的大领域。常见任务包括通过数据采集（DAQ）设备和传感器校准来连接硬件和软件。在实施控制系统之前，这两项任务都是必需的。 

QUBE-Servo 2仪器实验室概述

在QUBE-Servo 2课程中，您可以找到以下仪器实验室：

硬件整合

通常，“硬件集成（Hardware Integration）”实验室是学生第一次参加的实验。它奠定了基础-在这里，学生将学习QUBE-Servo 2硬件以及如何使用软件工具（例如Matlab / Simulink和QUARC实时控制软件）来与系统的电动机和传感器进行接口。

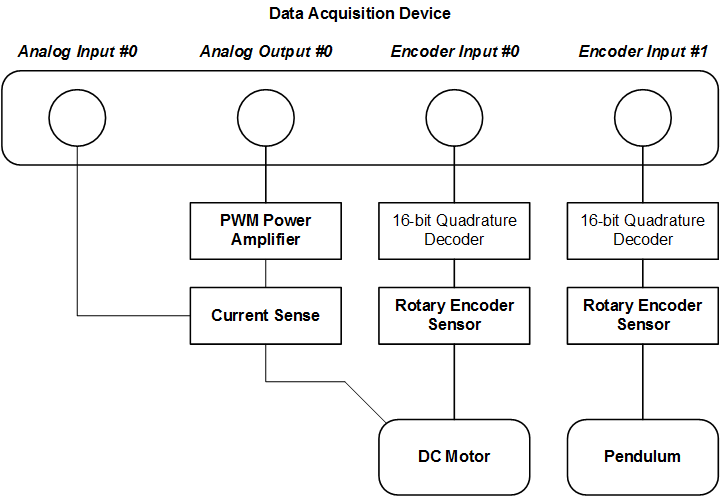
DAQ和QUBE-Servo 2 硬件之间的接口

滤波

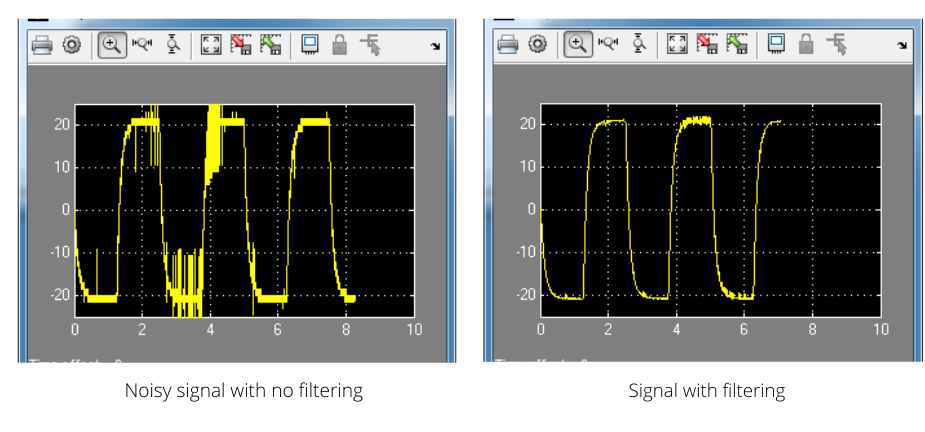
滤波在许多不同的行业中被广泛使用，经常在处理具有噪声并用于反馈控制的模拟传感器时使用。以QUBE-Servo 2过滤实验室为例，我们展示了从基于编码器的位置测量得出速度时如何需要过滤。下图将未经过滤的信号与经过过滤的版本进行了比较。您想在控制系统中使用哪一个？

为什么要建模？

通常需要获取系统模型（例如传递函数或状态空间表示形式），因此您可以使用它来设计控制系统。然后可以将模型用于运行仿真并验证是否满足系统要求。这增加了控制器在实际系统上工作的机会，并减少了设计迭代的次数。

QUBE-Servo 2建模实验室概述

下表总结了新旧的建模实验室。

实验建模

阶跃响应和频率响应是两种实验建模技术，有时称为“黑匣子”方法。这意味着他们不需要系统参数或系统的完整动态模型。它们通常用于动力学未知的系统，或者当模型太难从第一性原理推导时。通过检查输入信号和输出响应之间的关系可以找到模型。对于像QUBE-Servo 2这样的直流电动机系统，我们使用这些方法来识别一阶传递函数的参数，该参数表示电动机相对于所施加电压的位置或速度。

在阶跃响应建模（ Step Response Modeling）实验室中，通过在施加阶跃电压时检查输出电动机速度响应来得出模型，如下图所示。也称为“碰撞测试（bump test）”方法。

阶跃响应建模

频率响应是一种已使用多年的经典方法。在这种情况下，将频率可变的正弦波应用于系统。然后使用相应的正弦输出响应来构建波特图。由此，可以识别传递函数模型参数。下图显示了施加输入电压信号u并测量输出电动机速度响应y时的示例响应。

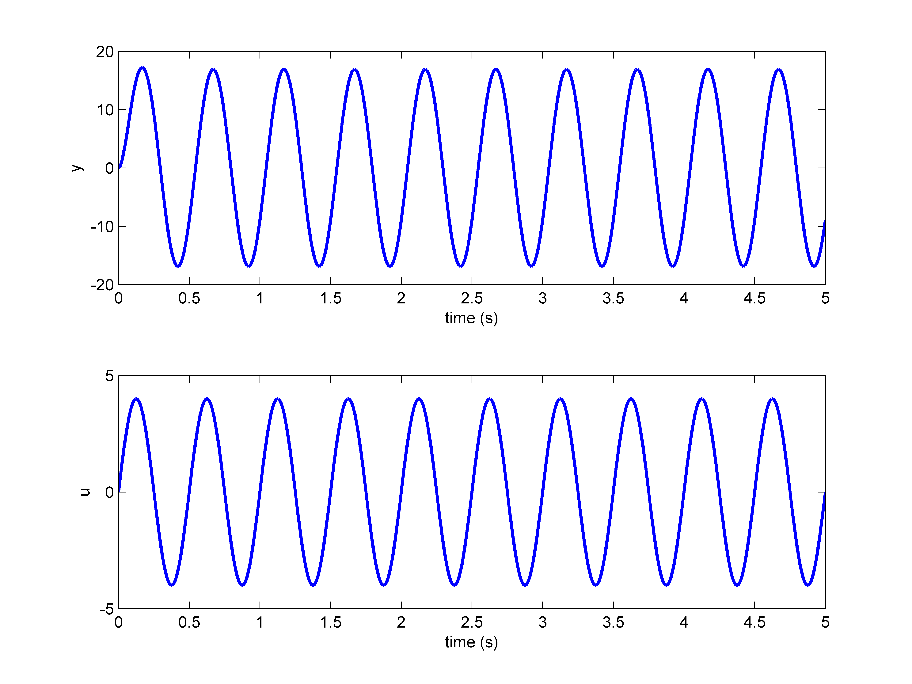
频率响应（Frequency response）

实验建模的利与弊

“黑匣子（Black box）”建模方法很好，因为它们执行时间不长（与从第一原理中得出的模型相比），并且还可以生成准确的模型。但是，它们的主要缺点是不能在不稳定的系统或有限制的系统上使用。例如，您不能使用阶跃响应在1 m的轨道上对推车进行建模，因为推车可能会到达终点站之一。

理论建模

当系统动力学已知时（例如QUBE-Servo 2的情况），我们可以使用类似于以下内容的自由图从第一原理推导其运动方程（EOM）：

QUBE-Servo2的型号

在框图建模（ Block Diagram Modelling）实验室中，使用标准Simulink块（例如，积分器和求和块）在Simulink图中实现QUBE-Servo 2模型。下面显示了一个框图示例。框图完成后，学生可以使用QUARC实时软件通过与硬件并行运行来验证模型是否正确。这称为“模型验证”。这是建模过程的重要组成部分，并且在所有QUBE-Servo 2建模实验室中都执行。

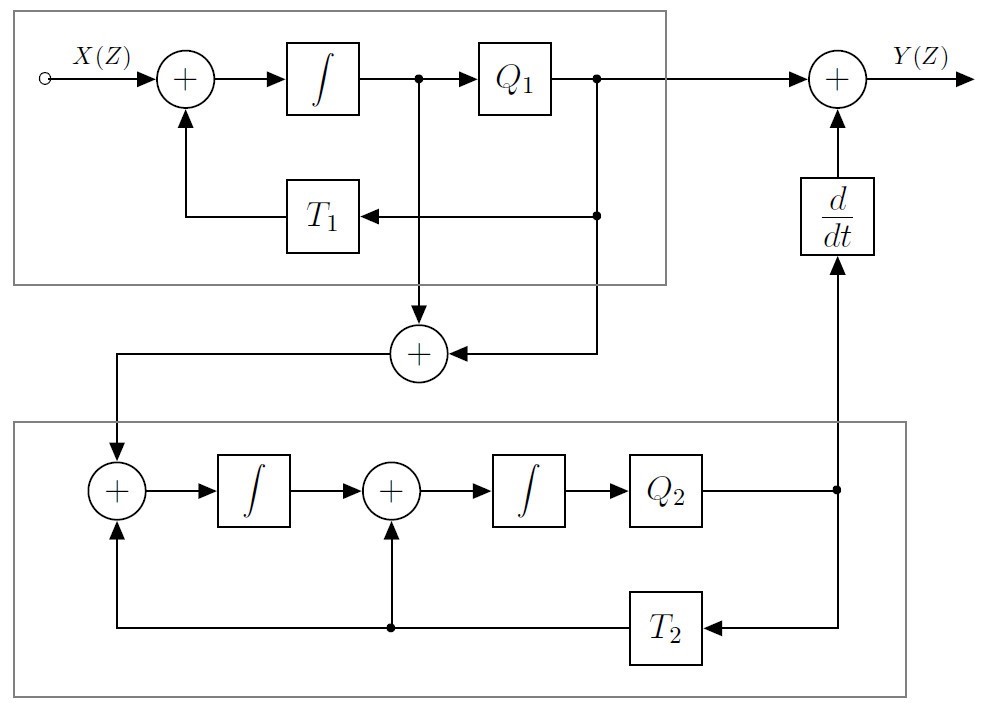
框图可用于为动力学已知的系统建模，例如QUBE-Servo 2。

理论建模的利与弊

使用框图从第一原理对系统进行建模需要深入了解组件之间的交互方式。您还需要了解系统参数（例如，电机轴惯量）。为了从第一原理对系统进行建模，还必须知道系统的动力学。此外，理论建模可能很难在复杂的系统上执行，并且可能会忽略例如实验建模方法中捕获的某些方面。

通过实验测试进行参数估计

在其他情况下，我们可能拥有模型，但是该模型的系统参数不可用或不准确。在“参数估计（Parameter Estimation）”实验室中，使用从第一性原理导出的方程式来获得评估电动机电阻和反电动势参数所需的方程式。但是，对于这些方程式，必须通过实验找到直流电动机的电动机电阻和反电动势参数。

参数估计的优缺点

参数估计方法结合了理论和实验建模的特点。仍然需要“了解系统”来推导模型，但是您不必知道所有系统参数。由于这些参数是通过实验找到的，而无需使用制造商的规格，这些规格在各个装置之间略有不同，因此可以获得更准确的模型。与“黑匣子”建模方法类似，主要缺点是参数估计仅在某些系统（例如非易失性系统）上可行。它还需要所有必要的传感器。例如，此实验无法在系统的早期版本QUBE-Servo 1上执行，因为它没有电流传感器。

模型表示

传递函数通常用于对许多系统进行建模，并且在大多数QUBE-Servo 2实验室中也使用。另一个常用的表示是状态空间。状态空间建模被应用于复杂度更高的多输入多输出（MIMO）系统，例如机械手。

新添加的状态空间建模（State-space Modelling）实验室是一种使用更简单的系统引入状态空间表示并将其通过验证模型是否准确表示系统来付诸实践的好方法。然后，这可能导致状态反馈控制，从而为更复杂的系统设计高级控制（例如，平衡不稳定的摆锤）奠定了基础。

非线性和无模型动力学

线性模型用于表征许多应用中的系统。但是，物理系统，数据采集设备等都具有在建模过程中被忽略的非线性元素。

在摩擦识别（Friction Identification experiment）实验中，我们重点介绍模型中最常被忽略的元素：库仑摩擦和粘滞摩擦。

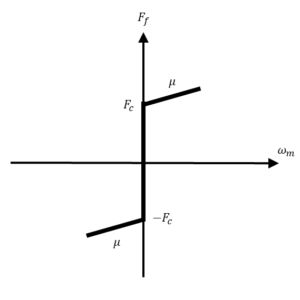
样本摩擦模型 

摩擦识别的利弊

大多数系统都有摩擦。知道摩擦如何影响系统响应是一个巨大的附加值，因为从模拟到在实际设备上实现其控制器时，这通常是学生首先注意到的：响应不匹配。但是在模型中不一定包括摩擦。实际上，通常将摩擦视为“可忽略的”，因为大多数应用程序都使用线性控制器。线性控制器设计基于线性模型，该模型不能包含非线性元素，例如库仑摩擦。另外，在初始设计之后，有相当简单的方法来补偿摩擦，例如，调整控制增益，添加积分控制。

希望本文能为您提供有关QUBE-Servo 2系统随附课程中的仪器和建模实验室的良好概述。

原文链接：https://www.quanser.com/blog/instrumentation-and-modelling-with-qube-servo-2/