资讯中心

Quanser的柔性尺旋转伺服系统是由一根柔性尺和SRVO2组成的2自由度的一个系统。这套设备可以用来比作很多现实生活中的应用譬如说在太空中的轻型机械臂、悬臂梁结构等等。下图则是我们这套系统的照片。

旋转伺服底座的角度测量是由一个增量型编码器所测得的，旋转的角度为Θ。柔性尺相对于伺服的角度α则是由一个在尺末端的应变计（strain gage）所测量的。

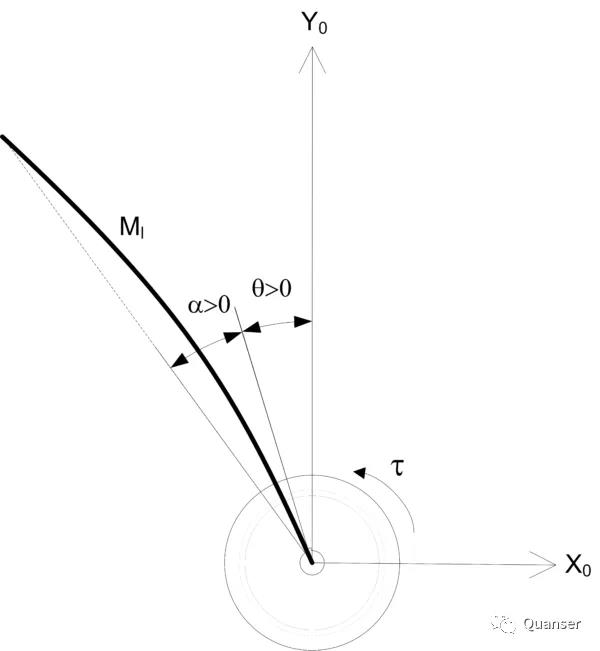
在这片文章中，我会主要介绍如何使用MathWorks的System Identification Toolbox 去识别柔性尺旋转伺服系统的线性状态空间模型。该模型接着会借助Control Systems Toolbox设计一个基于线性二次调节器的状态空间控制器。而控制器的目标则是需要：

控制伺服旋转到预定角度

柔性尺摆动最小化（因为伺服角度的变化）

整个闭环控制会在我们的QLabs虚拟柔性尺旋转伺服系统和和实际的硬件上进行。

系统辨识环节

在开始系统识别前，我们要确保柔性尺旋转伺服的设置正确。设置步骤如下：

确保柔性尺和伺服底座可以完全活动、没有任何障碍物

开始前柔性尺必须完全处于静止状态

确保应变计的连接线与柔性尺没有任何的缠绕，这会增加实验测量时的干扰

下图的Simulink模型使用了QUARC Real-Time Control Software和Simulink本身的应用结合组成的。我们使用了Signal Generator输出了一个方波电压信号然后去测量伺服和柔性尺的角度。我们的HIL Write Analog模块对直流电机输入电压后，再从HIL Read Timebase模块中读取编码器和应变计的度数。数据采集板卡则是一块单独的Quanser Q2-USB板卡。

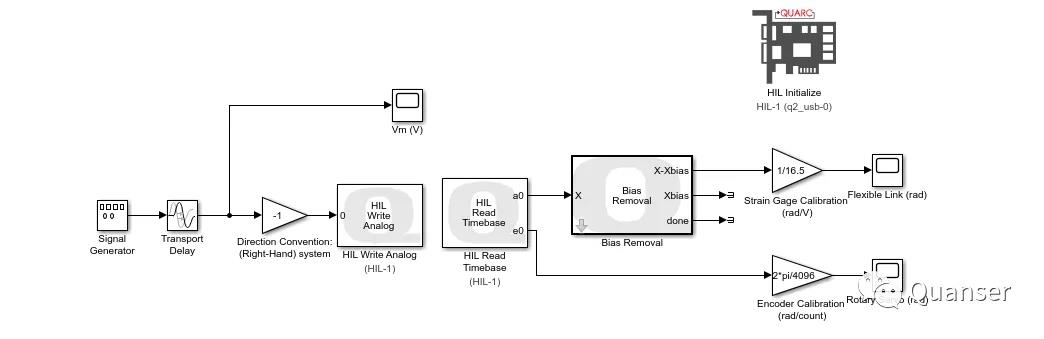
QUARC Bias Removal模块可以消除应变计的初始偏移量。电压输入、伺服和柔性尺的摆动角度都被记录保存为了MATLAB variables。这三组数据的结果如下：

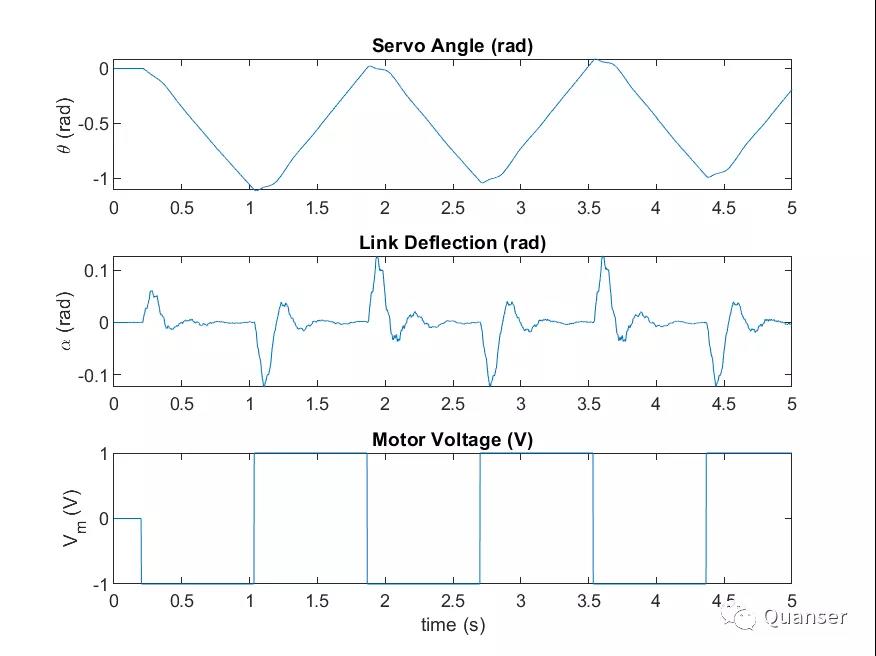
System Identification Toolbox的sset是用来计算线性状态空间模型的指令。识别出来的模型会通过compare指令与测量的结果做一个验证。

MeasuredData = iddata([theta,alpha],u,0.002);

[FlexlinkSS, IC] = ssest(MeasuredData,4);

compare(FlexlinkSS,MeasuredData);

如下图所示，识别出来的状态空间模型是非常准确的。

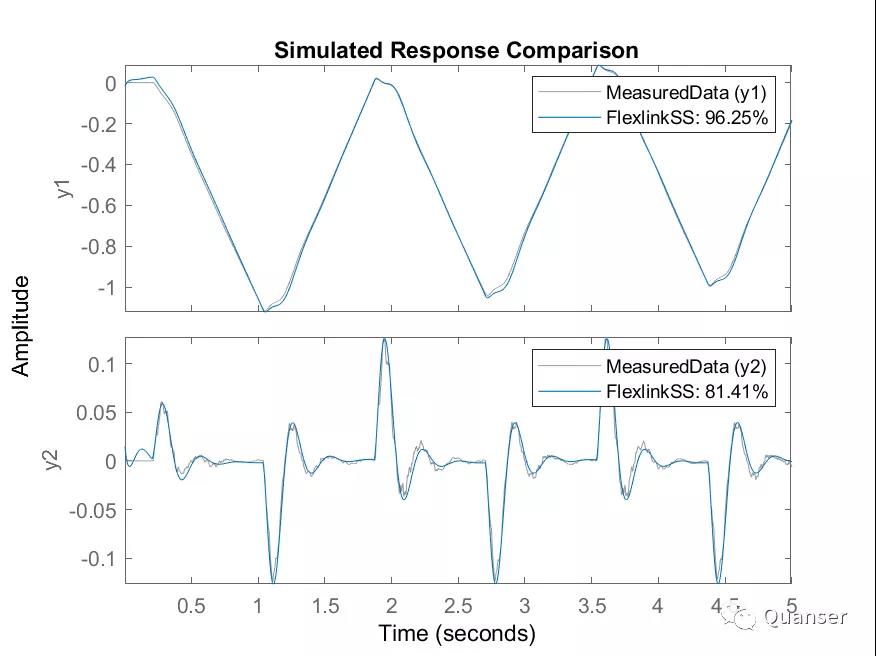
当然、System Identification Toolbox提供了很多其他的办法和模型。这次所使用的连续状态空间模型识别方法的一个特征就是不会强加任何的限制在A, B, C, D这四个系数上。

LQR控制器设计与闭环控制模拟

假设我们知道所有的状态，那么一个基于理想情况下的LQR的状态反馈控制器则可以完成：

控制伺服旋转角度到desired angle Θd

最小化柔性尺的余振（通过旋转伺服角度）

那么一个全状态反馈控制器则会是下面这个图标来表示：

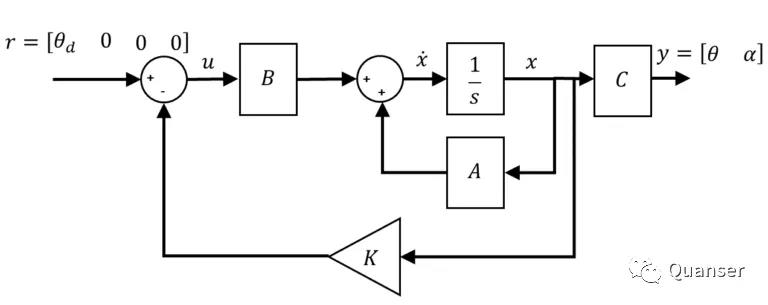
控制器可被看作为

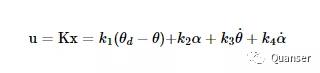
LQR的设计是使用MATLAB的LQR指令，结合识别的状态空间模型和经过对Q和R加权矩阵的调参所获得的。

% Save the identified state-space model as a standard MATLAB state-space

% system

sys_ol = ss(FlexlinkSS);

% Set Q and R LQR weighting matrices

Q = diag([500 0 0 2]);

R = 1;

% Generate feedback control gain using LQR

K = lqr(sys_ol,Q,R);

% Simulate the response in the Simulink model using the identified ss model

open("s_flexgage_control.slx");

sim("s_flexgage_control.slx");

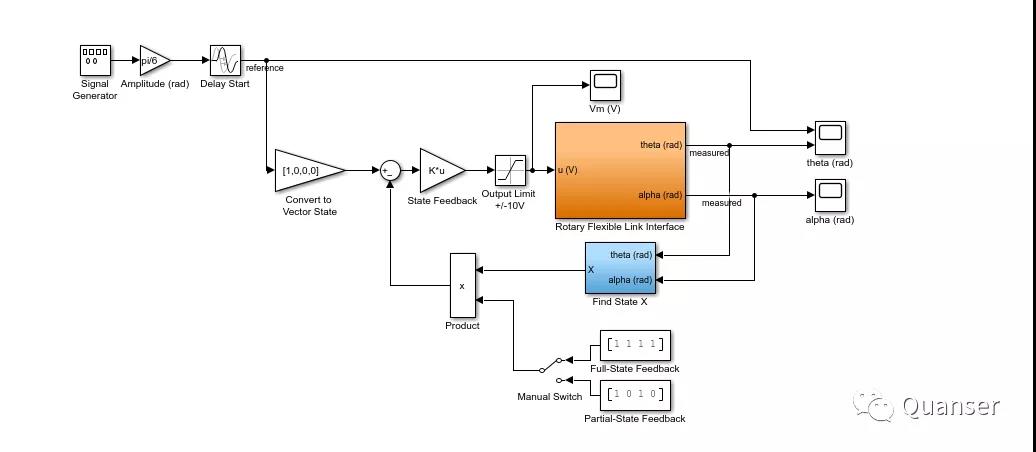
下图则是一个模拟的闭环控制器。Simulink的状态空间模型中已包含了识别的模型。

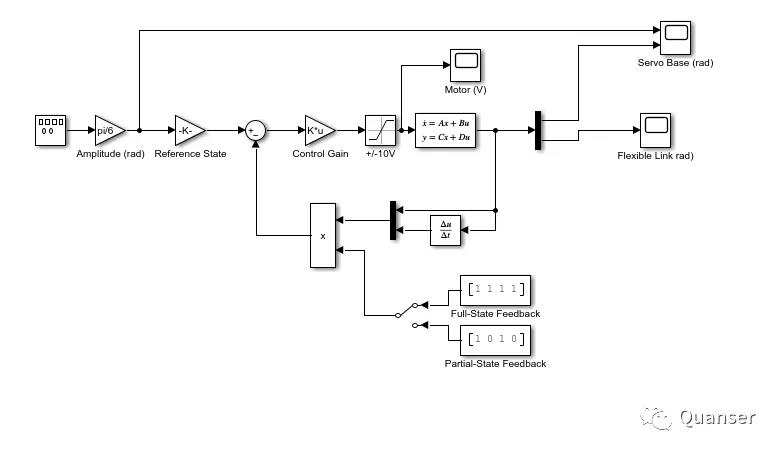
LQR 控制设计过程是迭代的。Q和R的加权矩阵在经过调参后可达到目标响应，即控制伺服角度到达指令角度的同时，减少柔性尺的摆动。电机的电压被控制在了正负10V。以下是当调参结束后的一段系统响应图的样本。

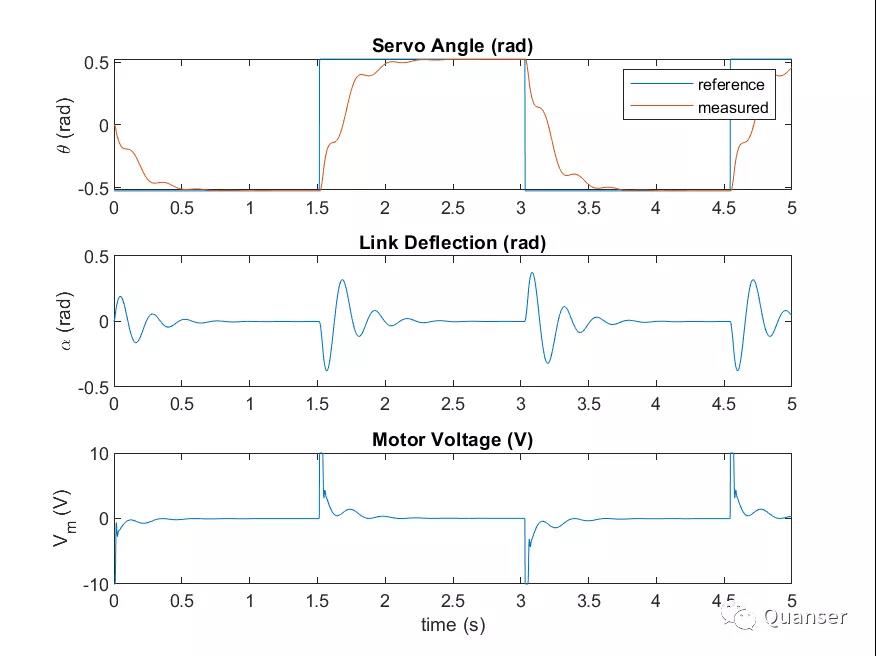
如上图所示，控制器能够跟踪伺服方波输入信号，以及减缓柔性尺的摆动，从而达到控制器的设计目标。

在Quanser虚拟柔性尺伺服系统上测试控制器

我们将LQR控制器现在虚拟硬件上做一个测试。这样可以确保控制器当出现重大设计错误时，不会有任何的损坏。我们基于数字孪生技术的硬件产品会更加贴近该产品的硬件表现。比原先的通过标准线性模拟出来的模型要更加的准确。在虚拟硬件上的Simulink模型如下图所示。

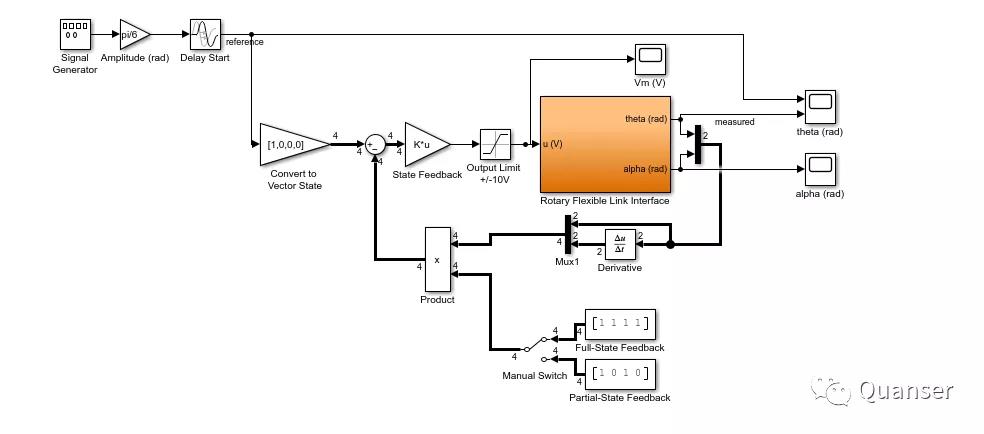
可以看到在这款虚拟的产品上的表现和之前线性模拟出来的表现非常接近。但是因为应变计上的信号干扰，在虚拟环境中我们会看到很多高频的波动。

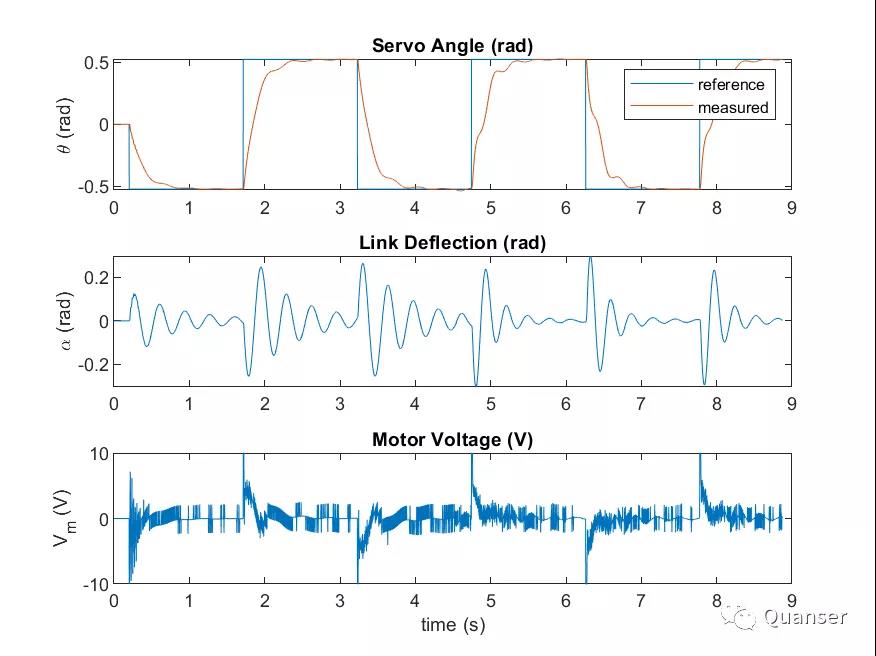
前3个周期是部分状态反馈的响应结果（当Simulink模型中Manual Switch拖到向下的位置时），在这个模式中，只有伺服的状态会被控制，所以控制器的公式就缩减成了：

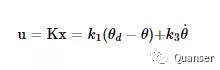
从这个公式中我们可以发现在partial的模式下，其实控制器就是对伺服做了一个经典的PD控制。

在后3个周期中则是使用了全状态反馈，那么这个时候控制器则要将柔性尺的摆动也要加进考虑中。

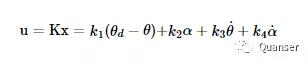
在这个模式种，柔性尺的摆动会随着伺服旋转角的变化而减少。

在硬件上测试控制器

在硬件上做完测试以后，同样的控制器现在则被放在了硬件上，我们依然会使用我们的QUARC Real-Time Control Software。

受限于应变计本身自带的干扰，柔性尺的摆动角和角速度的测量值都会被过滤。在硬件上的表现则是如下：

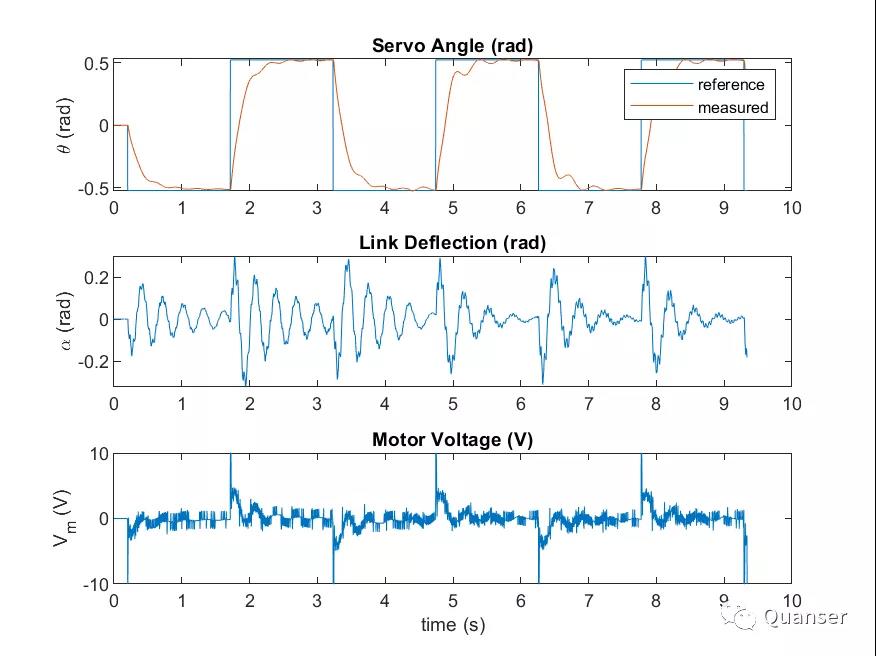
与数字孪生的柔性尺伺服一样，前3个周期是 部分状态反馈而后三个是全状态反馈。跟数字孪生的效果对比后，我们可以看到硬件上自带的很多信号干扰。虽然在数字孪生产品中，我们对所有的传感器都加入了信号干扰，但是这种信号干扰还是无法完全模拟硬件上的干扰形式，并且在数字孪生中，我们没有去模拟应变计连接线所带来的干扰。

说在最后

全状态反馈控制达到了将伺服角控制为所需命令的目标，同时最大限度地减少了柔性尺的摆动。 System Identification Toolbox 生成了非常准确的模型，可用于设计可用的控制器并节省大量开发时间。